Convolution
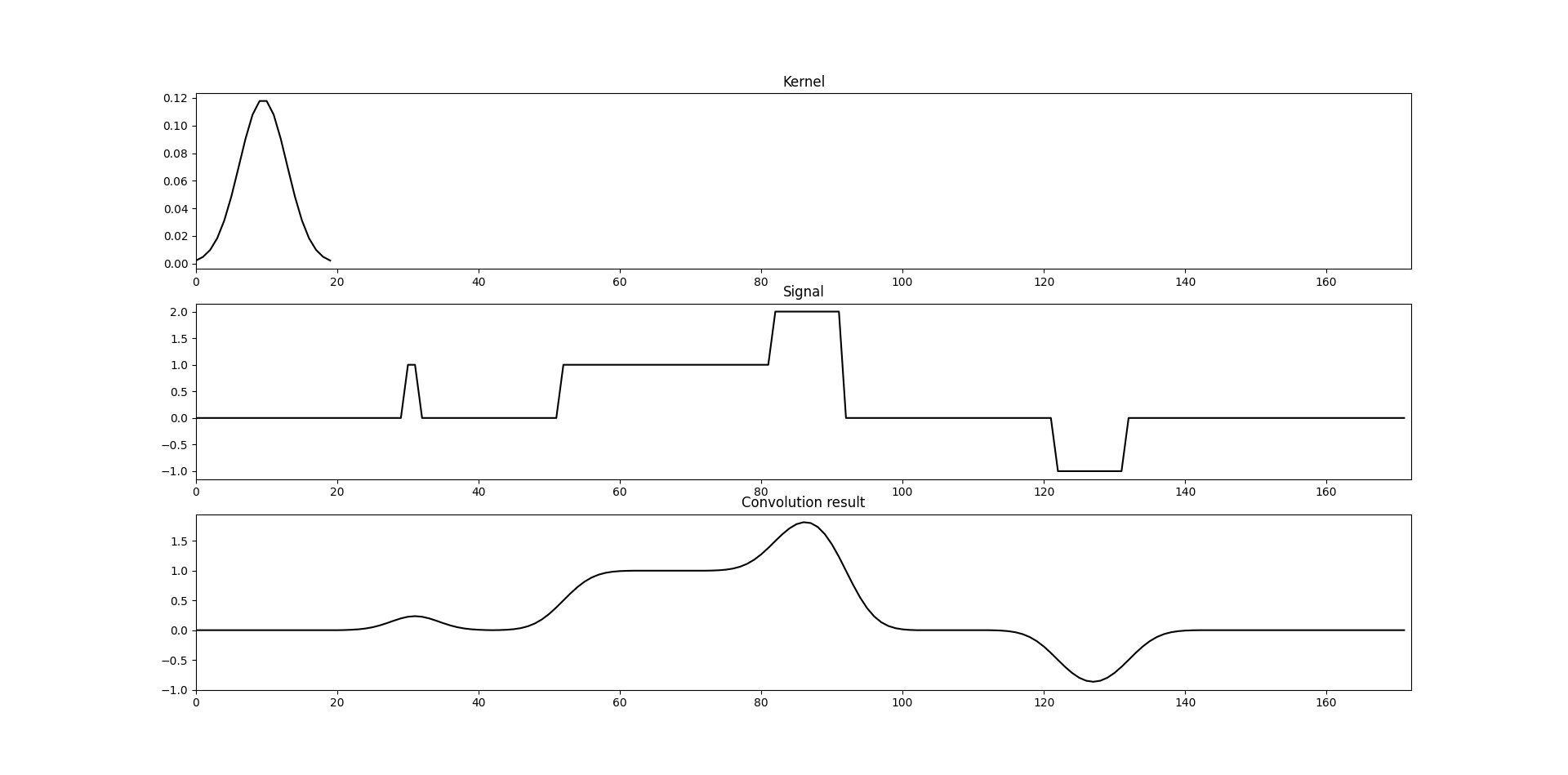
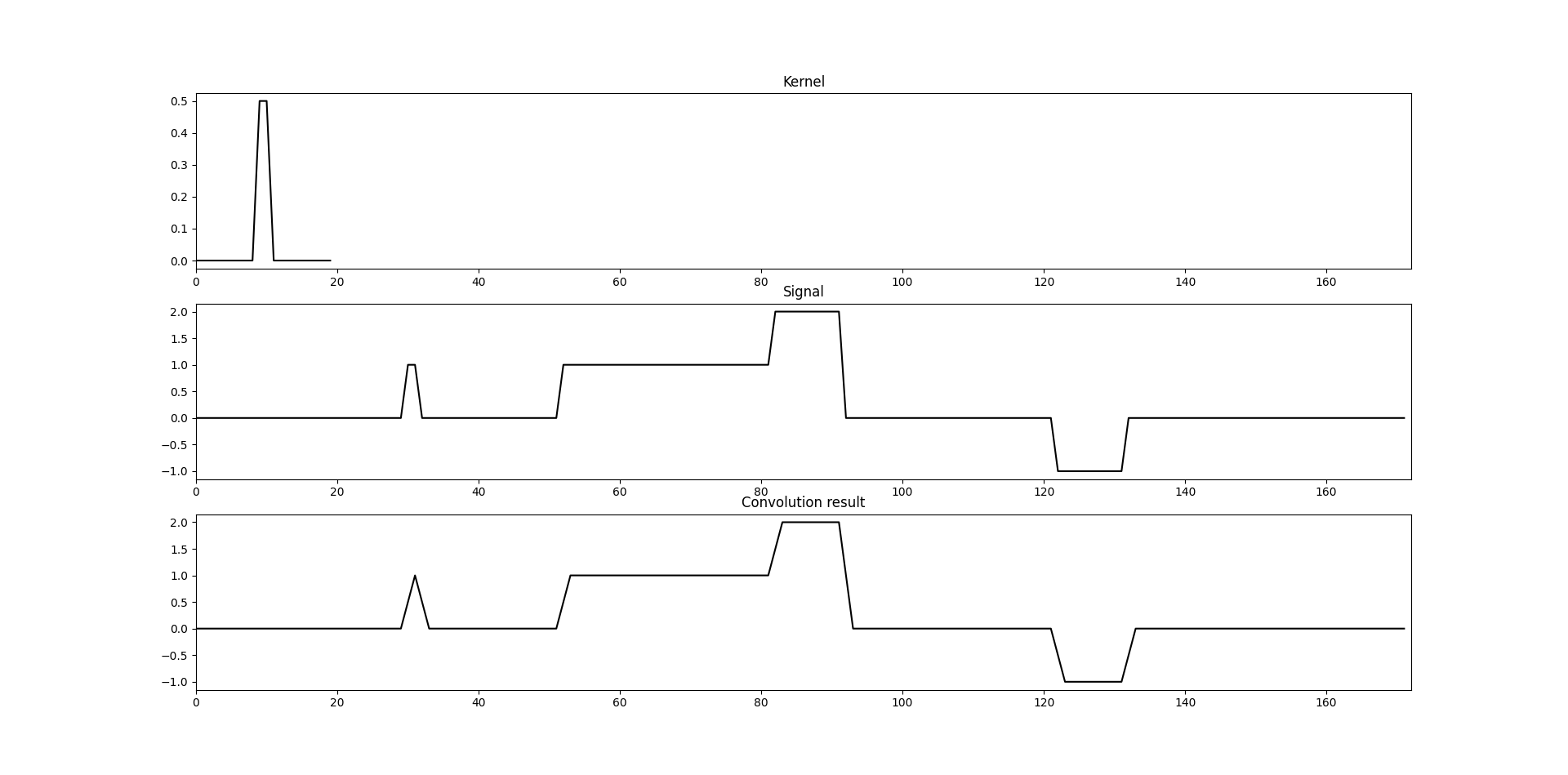
kernel_intuition
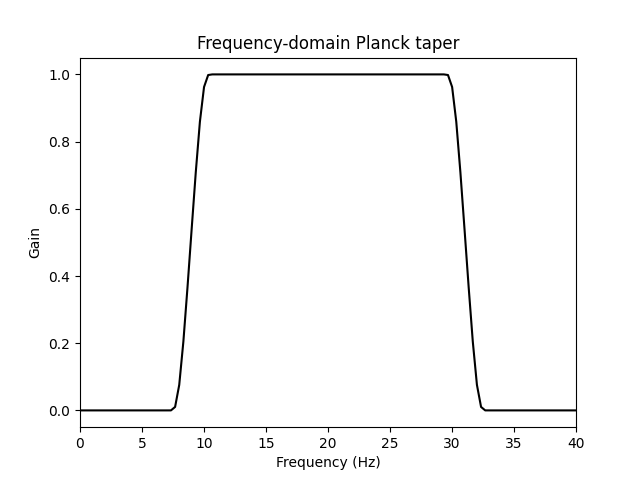
plank_taper
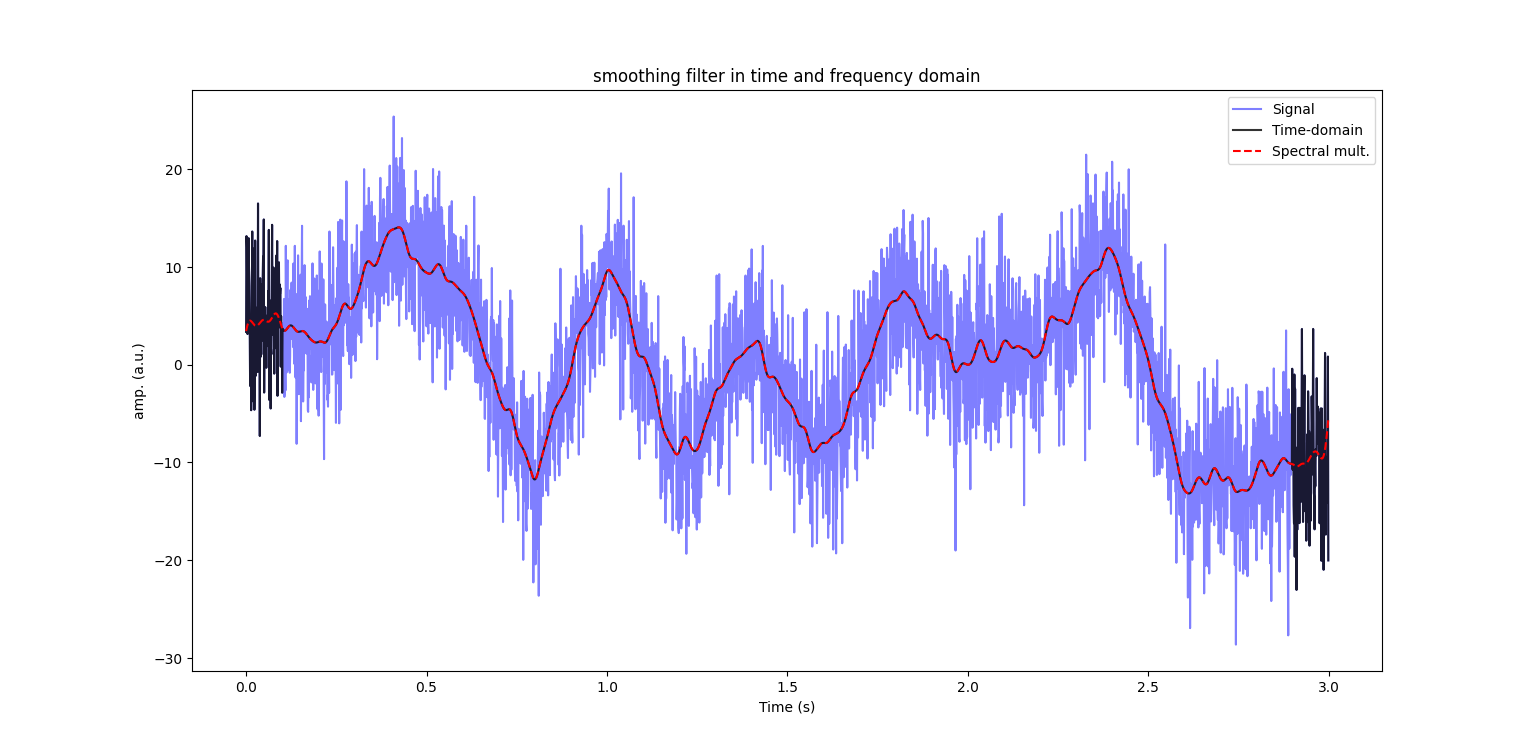
smoothing_filter_with_convolution
- smoothing_filter_convolution_example()[source]
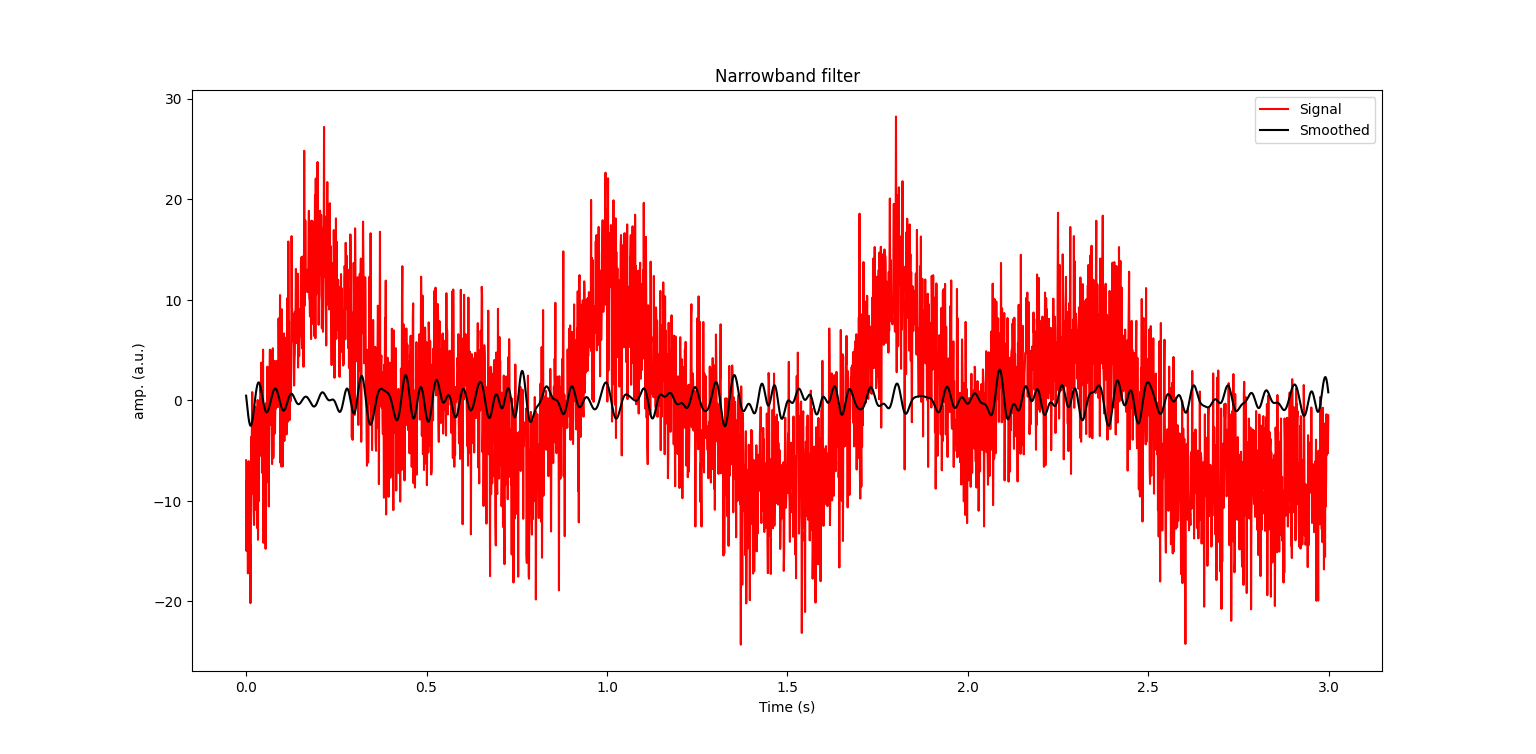
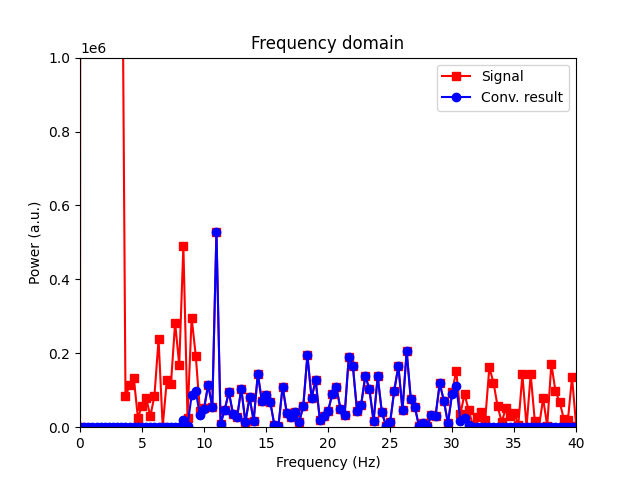
Smoothing filter and convolution theorem
A convolution in the time domain in equal to a multiplication in the frequency domain
- Time_domain :
- \[\text{fsignal} = \text{convolution}(\text{signal},\text{kernel})\]
- Frequency domain:
- \[\text{fsignal} = \text{ifft}(\text{fft}(\text{signal})*\text{fft}(\text{kernel}))\]