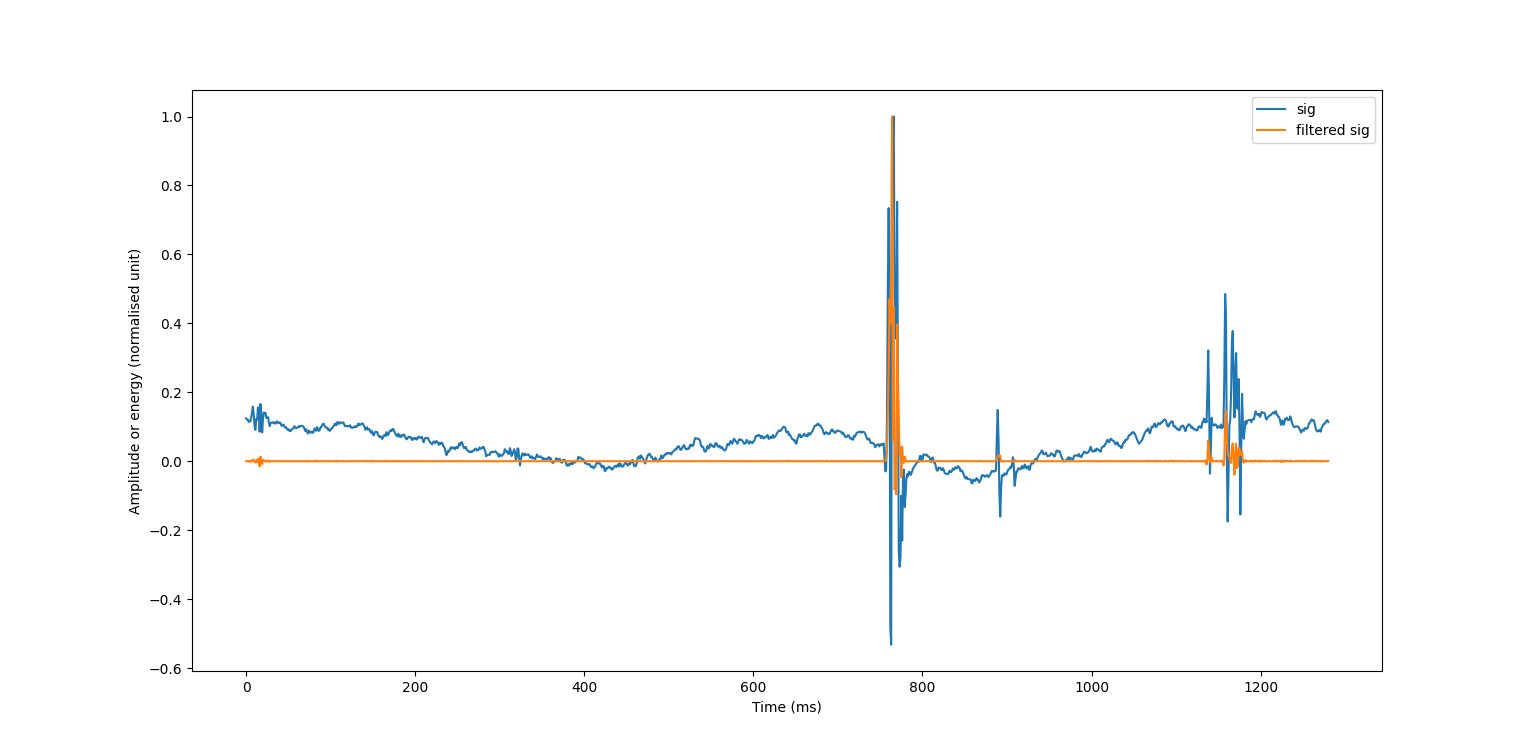
Time_series_denoising

Gaussian_smoothing_time_series_filter

gaussian_smoothing_filter(signal: ndarray, s_rate: int = 1000, k: int = 40, fwhm: int = 25) → Tuple[ndarray, int, int][source]

gaussian smoothing filter

Parameters:

signal (np.ndarray) – signal to be filtered
s_rate (int, optional) – sample frequancy. Defaults to 1000.
k (int, optional) – half window size. Defaults to 40.
fwhm (int, optional) – full width at half mawimum of the gaussian function. Defaults to 25.

Returns:

filtered_sig : signal filtered g : gaussian function used gtime : gaussian timestamps

Return type:

Tuple[np.ndarray, int, int]

gaussian_smoothing_filter_example()[source]

Example of the gaussian smoothing filter

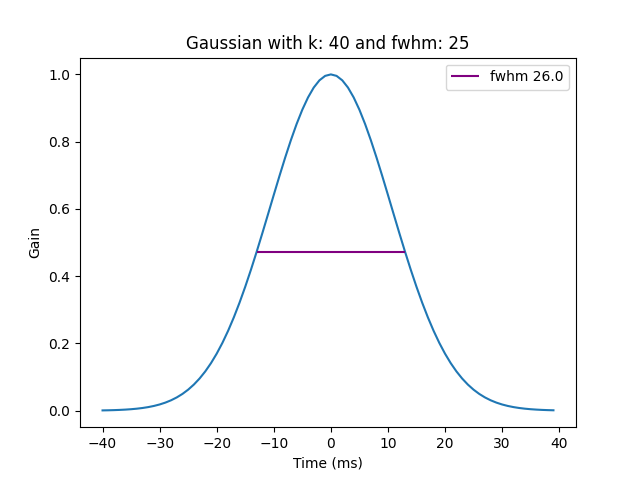
Two main faktor influence the gaussian smoothing filter:

the full width at half maximum (fwhm)
- influene the width of the guassian
the half window size (k)
- evenly split between right and left
- length of the window is therefore always an odd number
- influence the number of indexes of the gaussian kernel

The goal is to find the a good ratio between k and fwhm, knowing that k is also the sample window for filtering (the bigger k is the smoother the signal would be), so that the kurve look like a bell and to not have too much near 0 values on the right and left side

The fwhm is higlighted in the figure below:

The next two figures highlight the influence of the fwhm and k on:

the gaussian shape (=gaussian kernel)
and filtering of a example noisy signal

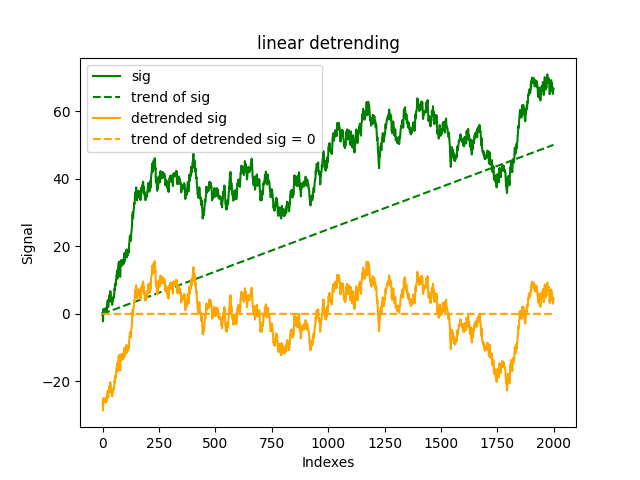
Linear_detrending

linear_detrending(sig: ndarray) → ndarray[source]

linear detrending function

Parameters:: sig (np.ndarray) – signal to be detrended
Returns:: detrended signal
Return type:: np.ndarray

linear_detrending_example()[source]

example of linear detrending usage

Remove the general trend of the data.

The iIdea is to fit a line that represent the golbal trend of the signal (green) and remove it from the signal. The mean value of the signal after detrending should be 0

Median_filter

median_filter_for_outliers(sig: ndarray, outlier_arr: ndarray, k: int = 20) → ndarray[source]

filter signals outliers using median value on a given window

Parameters:

sig (np.ndarray) – signal to be filtered
k (int, optional) – half window size. Defaults to 20.

Returns:

filtered signal

Return type:

np.ndarray

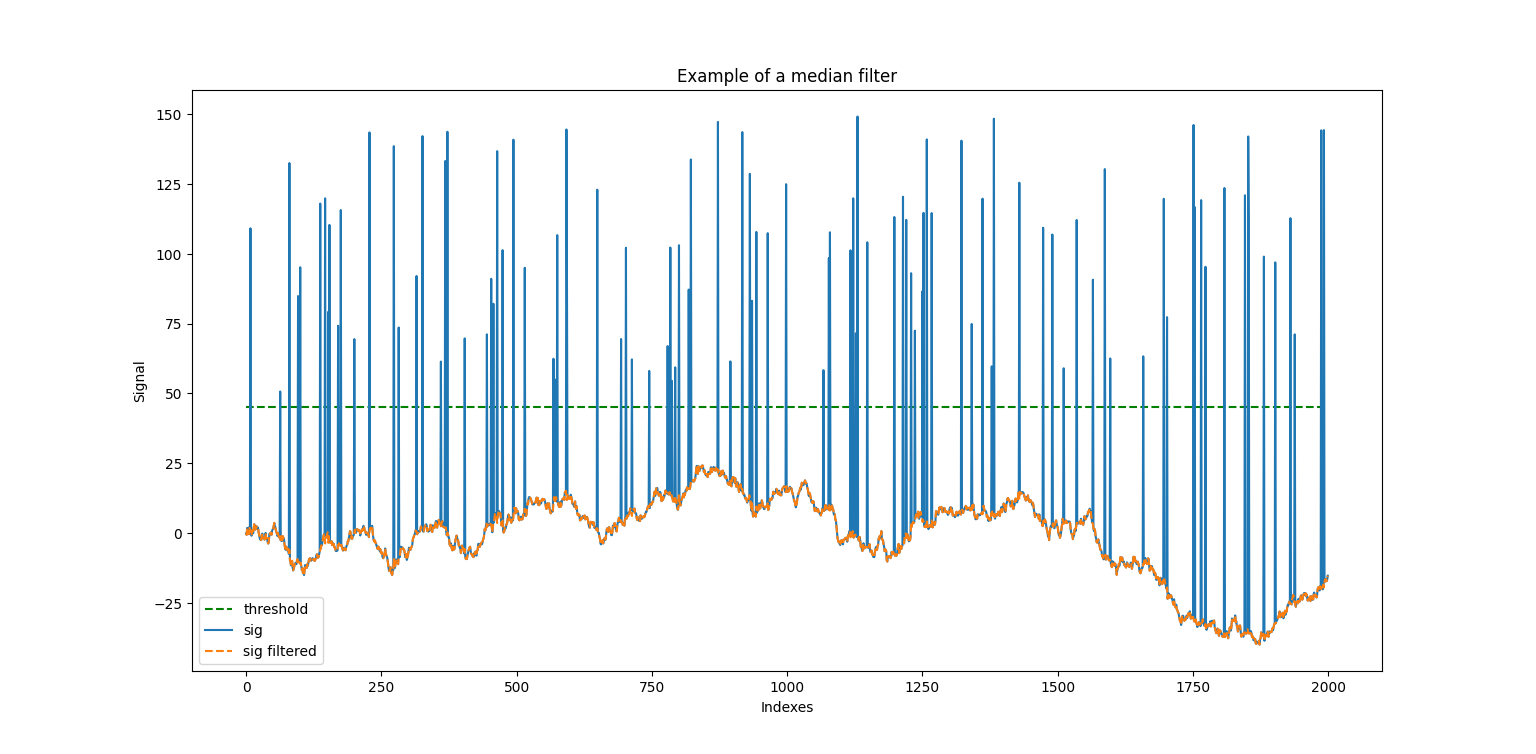
median_filter_for_outliers_example()[source]

example of filtering signal outliers using median value on a given window Median filter is less sensisitive to outlier - unusually high/low values., than mean/gaussian filtering

Median filter is a nonlinear filter It should be applied on selected data points and not on all data points → i.e define a threshold and replace all the value above it with a median value

Polynomial_detrending

polynomial_detrending_with_bayes_criterion(signal: ndarray, order_min: int = 2, order_max: int = 25) → ndarray[source]

polynomial detrending. Polynomial order defined based on bayes criterion

Parameters:

signal (np.ndarray) – signal to be detrended
order_min (int, optional) – min order of the polynomial. Defaults to 2.
order_max (int, optional) – max order of the polynomial. Defaults to 25.

Returns:

detrended signal

Return type:

np.ndarray

polynomial_detrending_with_bayes_criterion_example()[source]

Find best polynomial order with Bayes information criterion ():

Bayes information criterion (bic): Give an information about how close the y and y_fit are. We search for the minimal distance (red point on the figure below)

Formula:

\[bic =n \ln(\epsilon) + k \ln(n)\]

\[\epsilon = n^{-1} \sum^{n}_{i=1}(y_{fit, i} - y_i)^2\]

with:

k = polynomial order

y = raw signal

y_fit = predicted/fitted signal (=polynomial)

n = y length

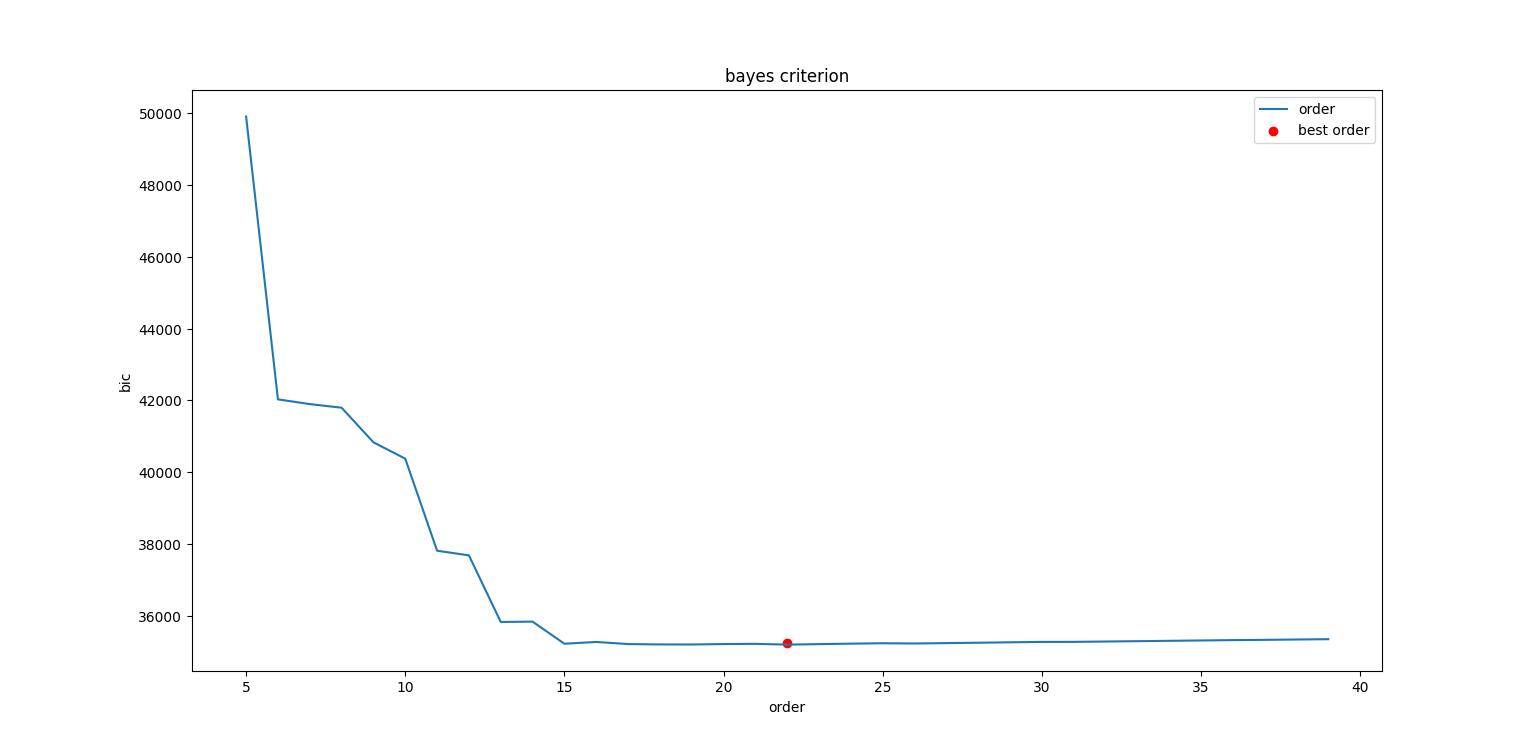
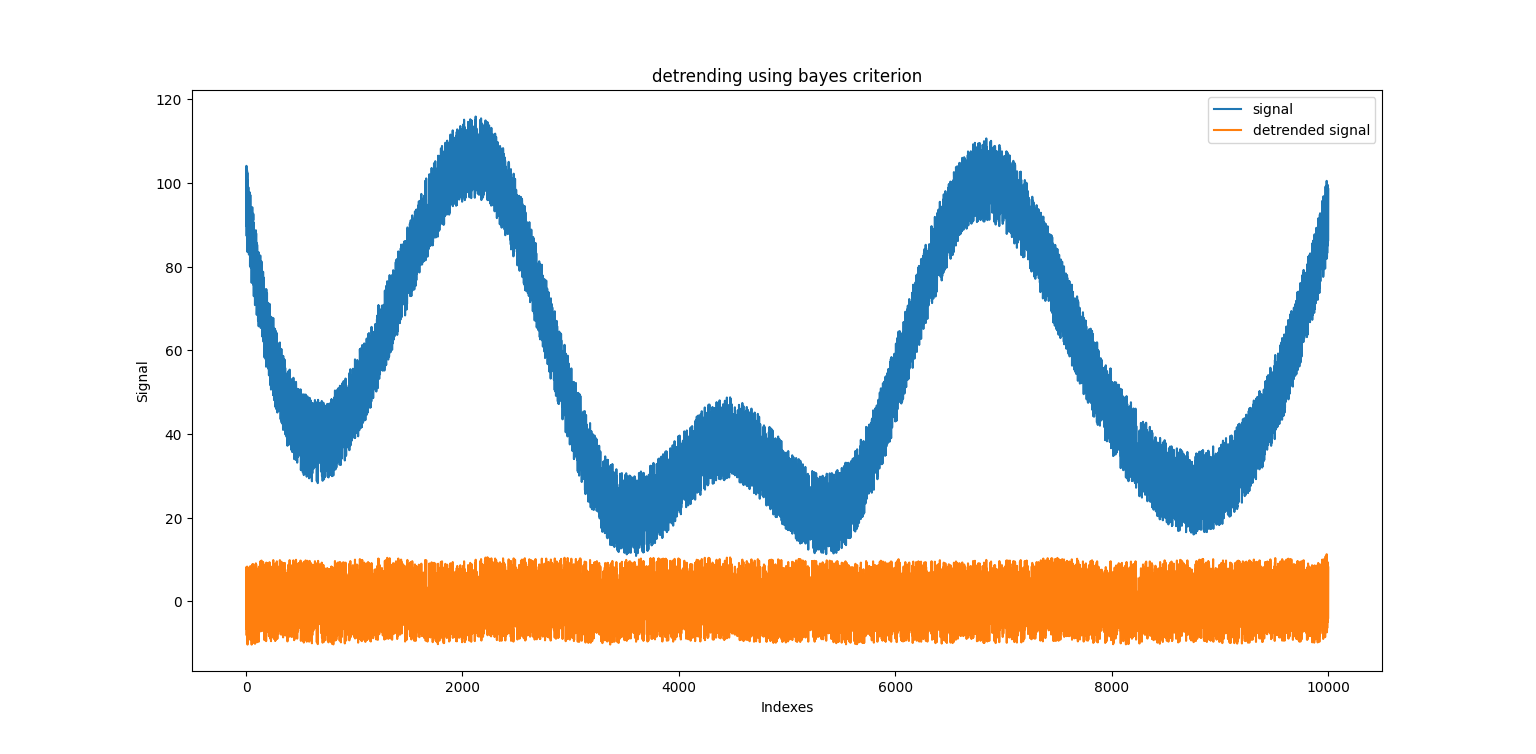
Detrending:: detreding is basically \(y - y_{fit}\).

understand_polynomials_orders()[source]: understand polynomial orders

Remove_artifact_with_last_squares

remove_artifact_with_last_square_between_two_signals(sig: ndarray, sig_artifact: ndarray) → ndarray[source]

remove an artifact from a signal using the last square method. The artifact is the sig_artifact.

Parameters:

sig (np.ndarray) – signal containing artifact that must be removed
sig_artifact (np.ndarray) – signal artifact

Returns:

signal without artifact

Return type:

np.ndarray

remove_artifact_with_last_square_between_two_signals_example()[source]

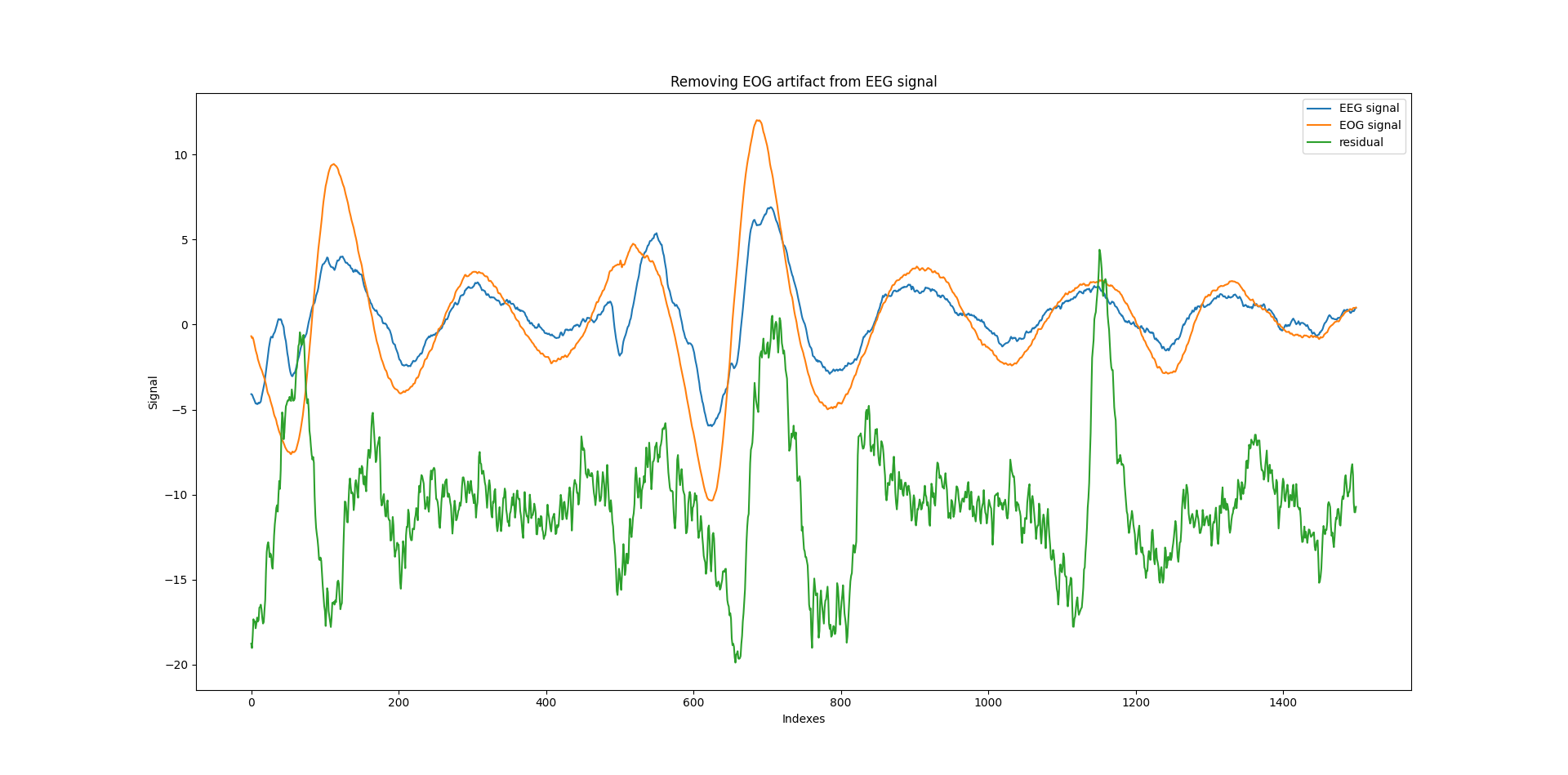
Example of removeing an artifact from a signal using the last square method:

Context:

EEG signal can be conain artifact because of the eyes movement (EOG signal).

Goal:

Remove the eye movement artifact

Method:

Use the last square template matching to remove the EOG artifact.

last square template matching:

\[\beta = (X^TX)^{-1}X^Ty\]

\[res = y - X\beta\]

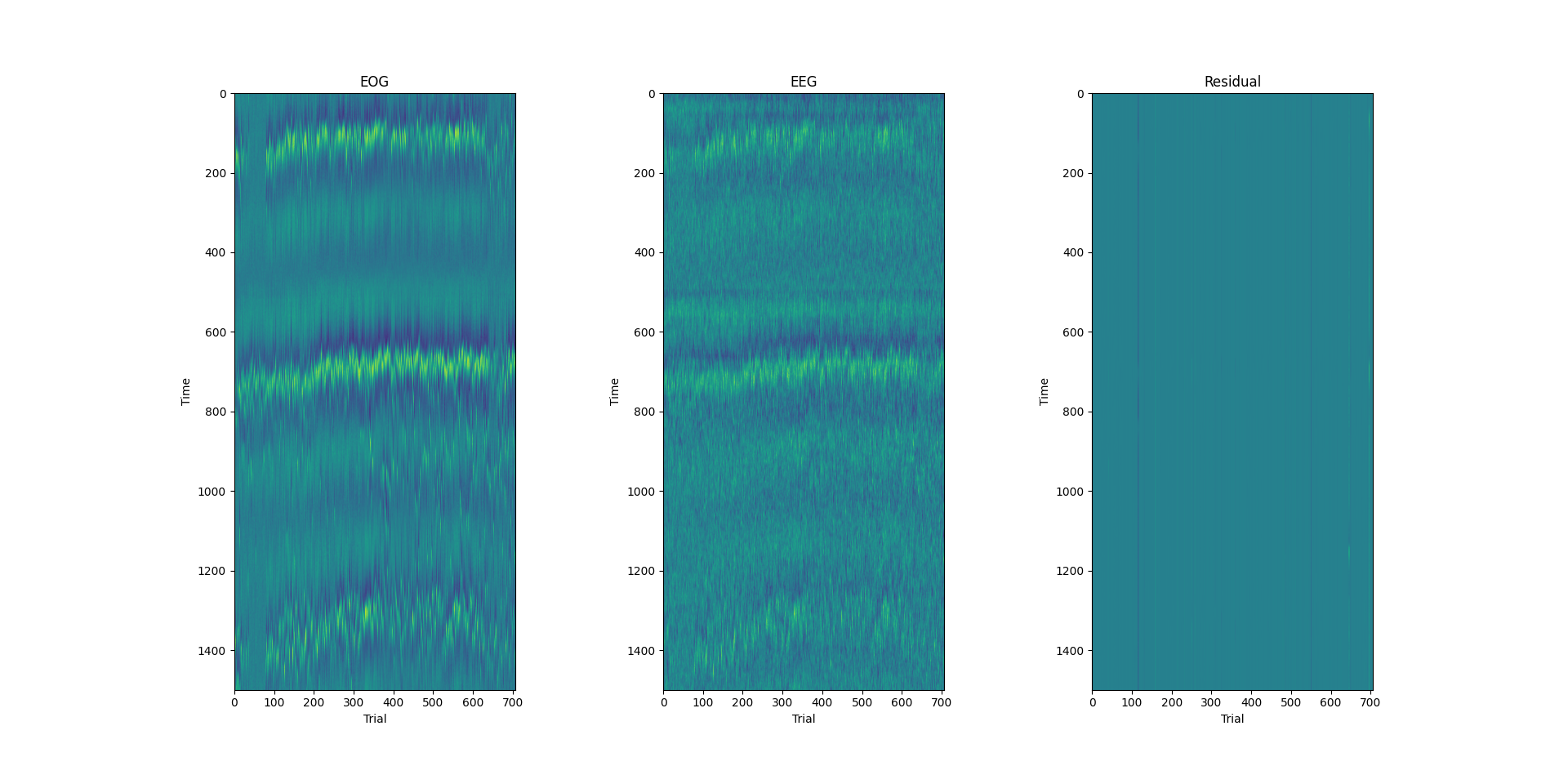
color map of the EOG, EEG, and residual signal:

Running_mean_filter

running_mean_filter(signal: ndarray, k: int = 20) → ndarray[source]

runnign_mean_filter

Parameters:

signal (np.ndarray) – signal to filter
k (int, optional) – half window size. Defaults to 20.

Returns:

filtered signal

Return type:

np.ndarray

running_mean_filter_example()[source]

example of running mean filter.

One faktor influence the running mean filter:

the half window size (k)
- evenly split between right and left
- length of the window is therefore always an odd number
- influence the number of indexes of the gaussian kernel

The effect of k is highlighted on the figure below:

TKEO

TKEO(sig: ndarray) → ndarray[source]

Teager kaisor operator on a given signal

Parameters:: sig (np.ndarray) – signal to filter
Returns:: filterd signal
Return type:: np.ndarray

TKEO_example()[source]

Teager kaisor operator example

Context:: EMG data is often noisy, We want to focus on a particular events that append.
Method:: TKEO will amplify/highly phases with high energy changes.

time_synchronous_averaging

time_synchronous_average_example()[source]