Filtering

FIR

FIR_filter_example()

Example of FIR filter for a narrowband filter

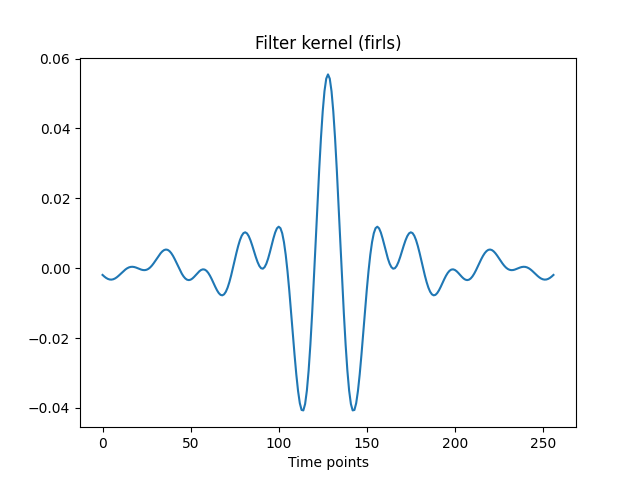
1. Creation of the filter kernel using FIR funtion

• Creation of the input of the FIR function

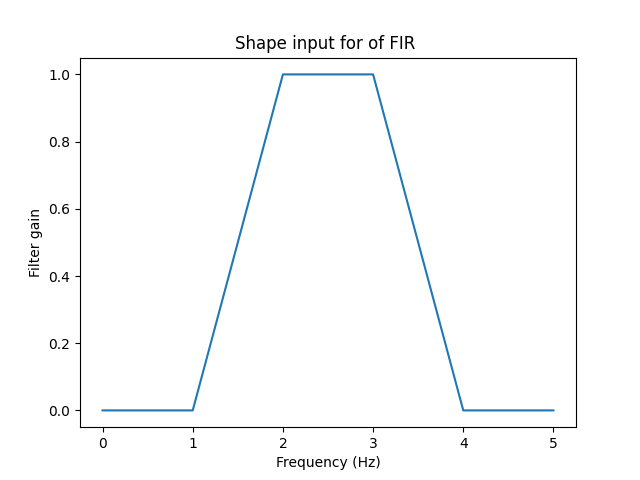
• Output of the FIR function is the kernel

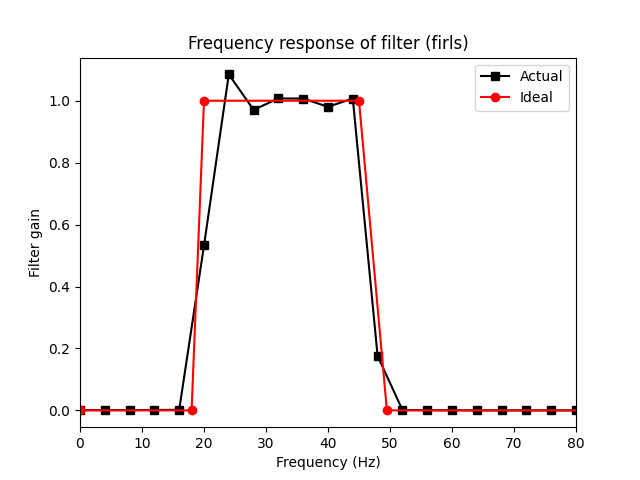
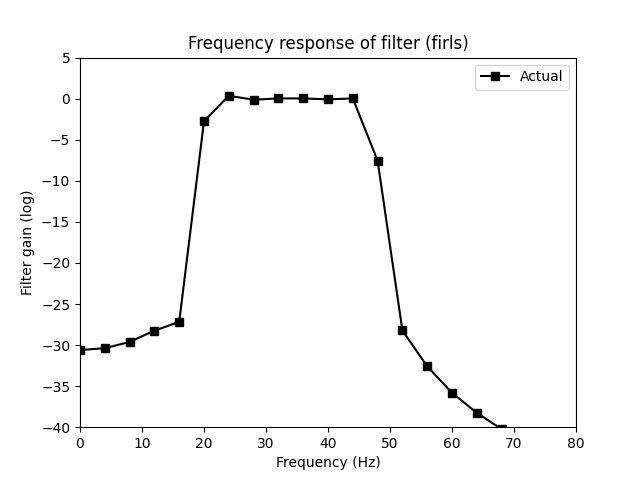
2. Analysis of the frequency response

• Analysis of the frequency response in comparison of the ideal response

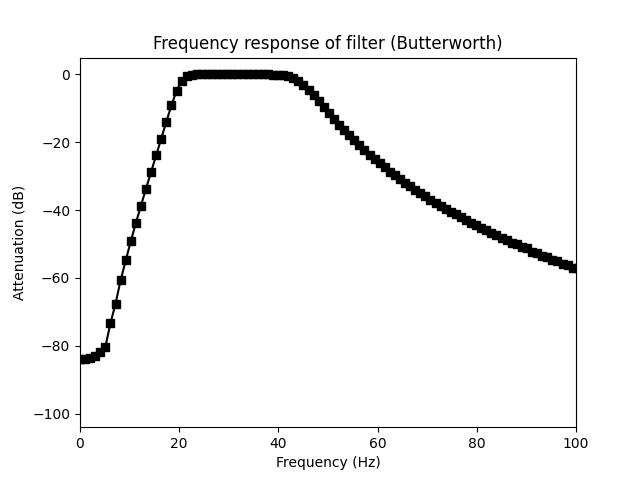
• In dB (it allows to see more details)

FIRwin_eample()

IIR

IRR_filter()

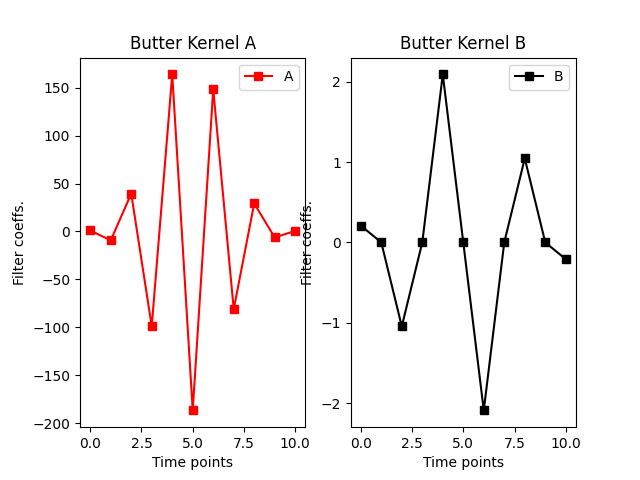
1. Creation of the filter kernel using butter funtion

The IRR filter are composed of two kernel, often call “a” and “b”.

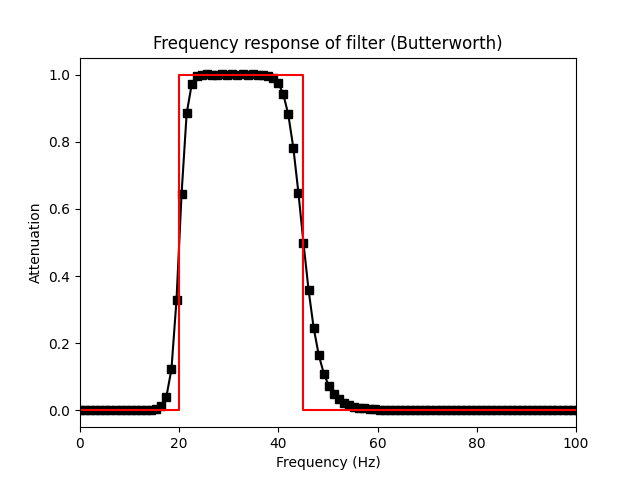
2. Analysis of the frequency response

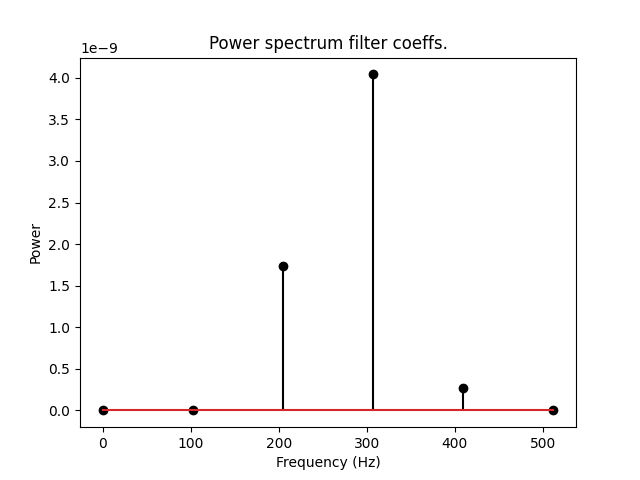
As IRR kernel are from very little order (comparing to FIR)

e.g. butter filter from order 4 means the Kernel signal will be composed

of only 4*2+1 points. These lead in only 6 point in the frequency domain.

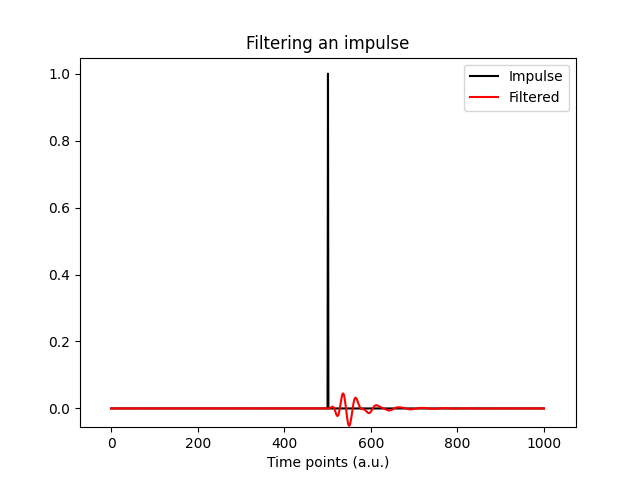
A better way to evaluate the kernel function is to filter a basic impulse response (arr = [0, 0, 1, 0, 0]) and take a look at its frequency response

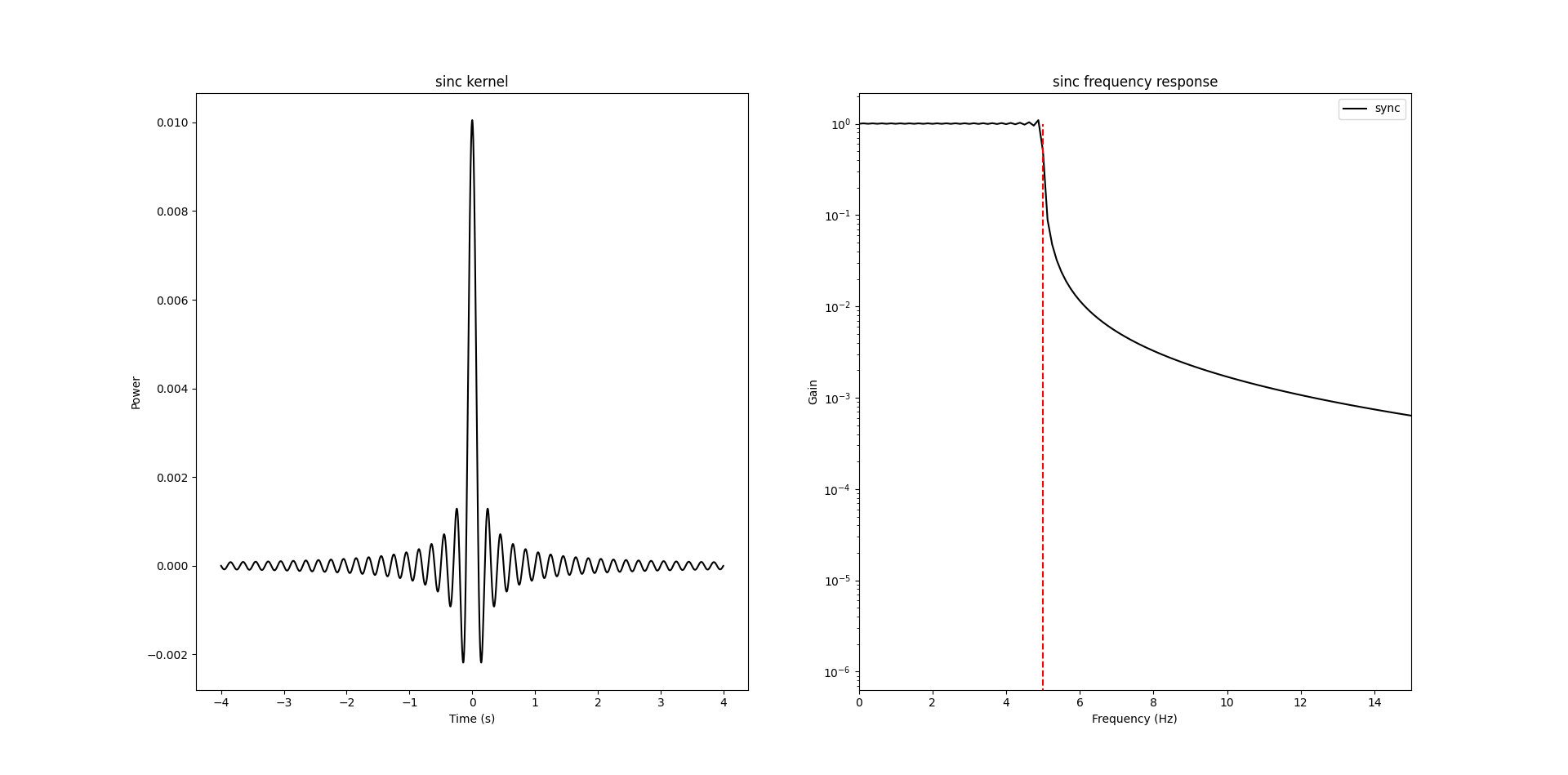
WindowedSinc_filter

filter_data_with_sinc_window_filter_example()

Example of the windowed sinc low pass filter on real signal:

sinc_filter_example()

\[\text{sinc}(t) = \frac{\sin(2 \pi f_c t)}{t}\]

with

\[f_c : \text{cut-off frequency}, t : \text{timestamps}\]

sinc_window_filter_example()

The sinc filter can be improved by multipling a window with itself.

Different window exist with different caracteristics:

• Hann (hanning)

• Hamming

• Gaus

frequency_domain_normalisation

relfection

roll_off