Clustering ascendant hierarchique
1.1 Context
Ce notebook est en lien le chapitre l’activité Effectuez une classification hiérarchique, de la partie 3 du cours Réalisez une analyse exploratoire de données.
Nous allons travailler sur le jeu de données iris.
1.2 Imports
Importons les librairies :
[1]:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
1.3 Graphics
Chargeons les librairies graphiques :
[2]:
sns.set()
1.4 Data
Chargeons les données. Nous utiliserons le dataframe iris, directement présent dans scikit-learn.
Il faudra travailler un peu pour pouvoir l’utiliser correctement. Ne pretez pas trop attention aux lignes ci dessous.
[3]:
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df.columns = [i.split('(')[0].replace(" ", "_")[:-1] for i in df.columns]
X=df.copy()
X.head()
[3]:
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 |
[4]:
X.shape
[4]:
(150, 4)
2. About ACH
Effectuons une classification hiérarchique ascendante.
2.1 Compute linkage
Nous allons calculer les distances en spécifiant la méthode à utiliser:
[5]:
Z = linkage(X, method="ward")
pd.DataFrame(Z)
[5]:
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 101.0 | 142.0 | 0.000000 | 2.0 |
| 1 | 7.0 | 39.0 | 0.100000 | 2.0 |
| 2 | 0.0 | 17.0 | 0.100000 | 2.0 |
| 3 | 9.0 | 34.0 | 0.100000 | 2.0 |
| 4 | 128.0 | 132.0 | 0.100000 | 2.0 |
| ... | ... | ... | ... | ... |
| 144 | 282.0 | 290.0 | 3.828053 | 50.0 |
| 145 | 287.0 | 288.0 | 4.847709 | 36.0 |
| 146 | 292.0 | 293.0 | 6.399407 | 64.0 |
| 147 | 295.0 | 296.0 | 12.300396 | 100.0 |
| 148 | 294.0 | 297.0 | 32.447607 | 150.0 |
149 rows × 4 columns
[6]:
pd.DataFrame(Z).iloc[:10,:]
[6]:
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 101.0 | 142.0 | 0.000000 | 2.0 |
| 1 | 7.0 | 39.0 | 0.100000 | 2.0 |
| 2 | 0.0 | 17.0 | 0.100000 | 2.0 |
| 3 | 9.0 | 34.0 | 0.100000 | 2.0 |
| 4 | 128.0 | 132.0 | 0.100000 | 2.0 |
| 5 | 10.0 | 48.0 | 0.100000 | 2.0 |
| 6 | 4.0 | 37.0 | 0.141421 | 2.0 |
| 7 | 19.0 | 21.0 | 0.141421 | 2.0 |
| 8 | 29.0 | 30.0 | 0.141421 | 2.0 |
| 9 | 57.0 | 93.0 | 0.141421 | 2.0 |
2.2 Dendrograms
Nous pouvons désormais afficher le dendrogramme:
[7]:
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
_ = dendrogram(Z, ax=ax)
plt.title("Hierarchical Clustering Dendrogram")
plt.xlabel("Number of points in node (or index of point if no parenthesis).")
plt.ylabel("Distance.")
plt.show()
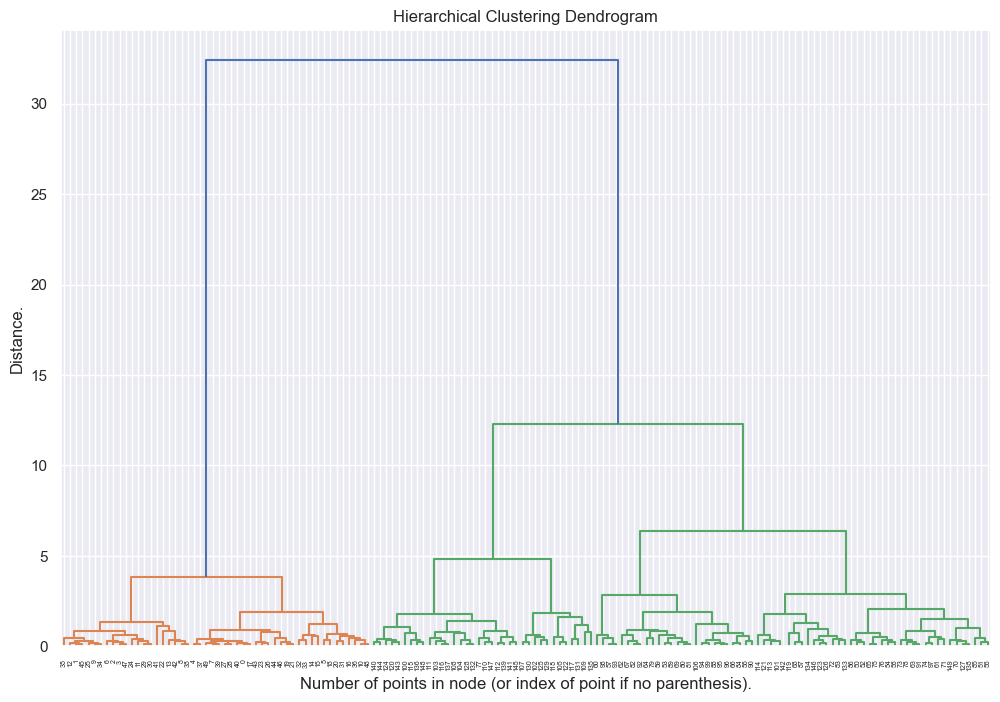
Le dendrogramme semble pertinent mais sa profondeur le rend illisible.
On peut jouer sur différents paramètres pour obtenir un dendrogramme plus lisible :
[8]:
# les arguments p=10, truncate_mode="lastp" signifient que l'on ne va afficher que 10 clusters
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
_ = dendrogram(Z, p=10, truncate_mode="lastp", ax=ax)
plt.title("Hierarchical Clustering Dendrogram")
plt.xlabel("Number of points in node (or index of point if no parenthesis).")
plt.ylabel("Distance.")
plt.show()
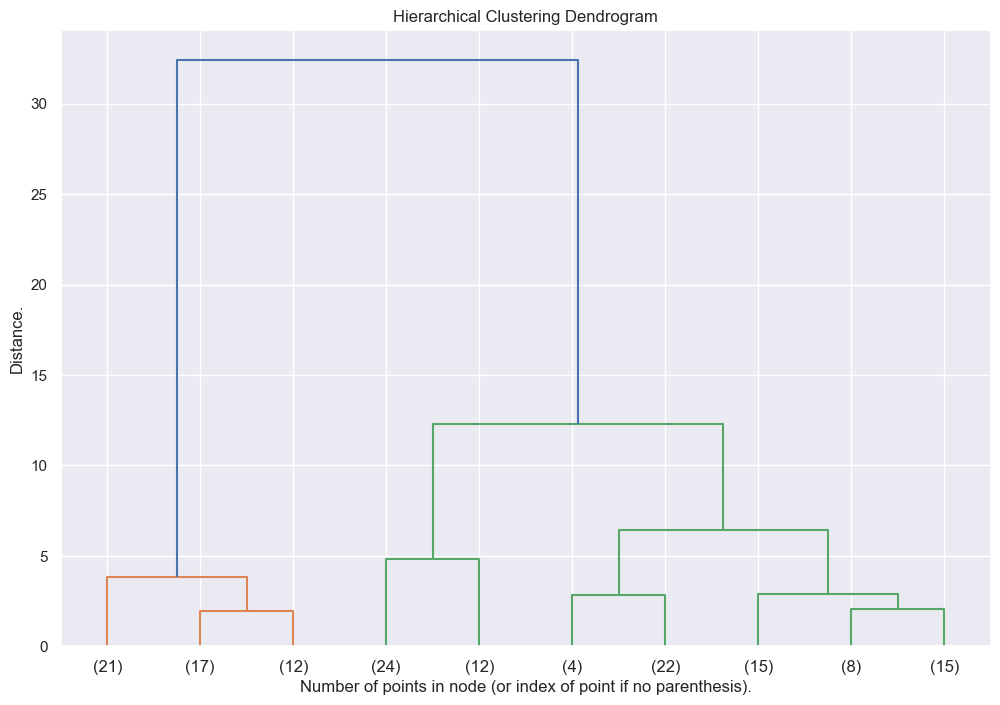
[9]:
# les arguments p=3, truncate_mode="level"signifient que l'on ne va afficher que les clusters issus de 3 noeuds.
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
_ = dendrogram(Z, p=3, truncate_mode="level", ax=ax)
plt.title("Hierarchical Clustering Dendrogram")
plt.xlabel("Number of points in node (or index of point if no parenthesis).")
plt.show()
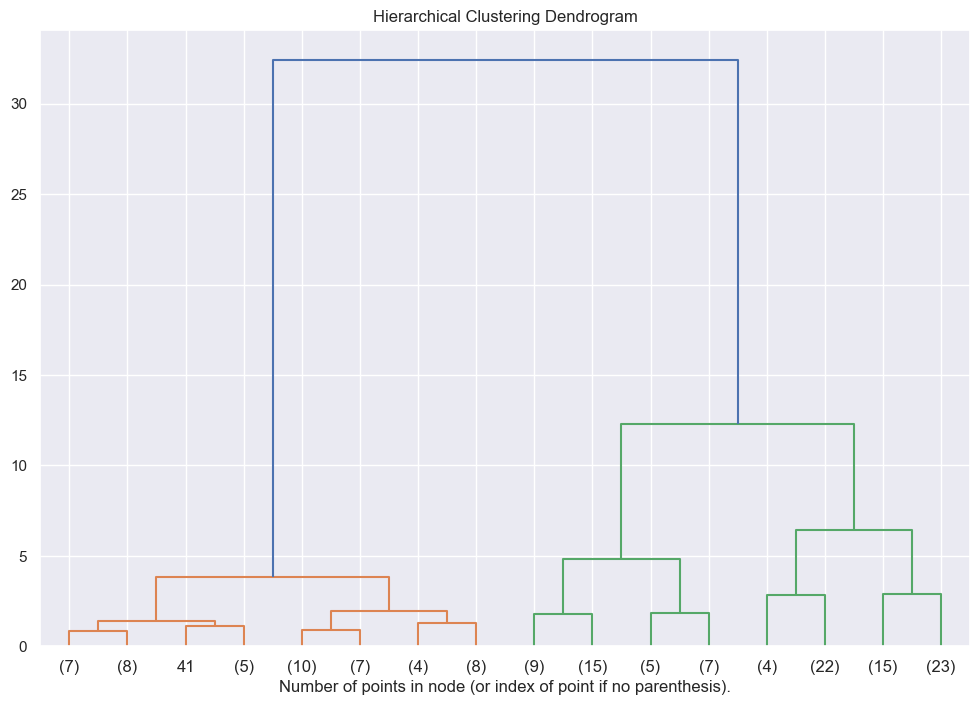
2.3 Clusters
Pour définir les clusters, on peut utiliser scipy ou scikit-learn.
2.3.1 Scikit-Learn
On instancie un estimateur :
[10]:
cah = AgglomerativeClustering(n_clusters=3, linkage="ward")
On entraine l’estimateur :
[11]:
cah.fit(X)
[11]:
AgglomerativeClustering(n_clusters=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
AgglomerativeClustering(n_clusters=3)
Regardons nos clusters :
[12]:
cah.labels_
[12]:
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2,
2, 0, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0], dtype=int64)
0,1,2 est à considérer comme une variable catégorielle cardinale. Il n’y a pas d’ordre entre les clusters.Le cluster 0 n’est pas supérieur au cluster 1 par exemple. Considérez que c’est plus un id qu’une valeur.
Pour être plus clair, nous allons utiliser des lettres plutôt que des nombres:
[13]:
dd = {i:j for i,j in enumerate(list("abc"))}
labels = [dd[i] for i in cah.labels_]
labels[:10]
[13]:
['b', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b', 'b']
Disons que c’est plus clair maintenant…
Ajoutons nos labels à X
[14]:
X["cluster"] = labels
X.head()
[14]:
| sepal_length | sepal_width | petal_length | petal_width | cluster | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | b |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | b |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | b |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | b |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | b |
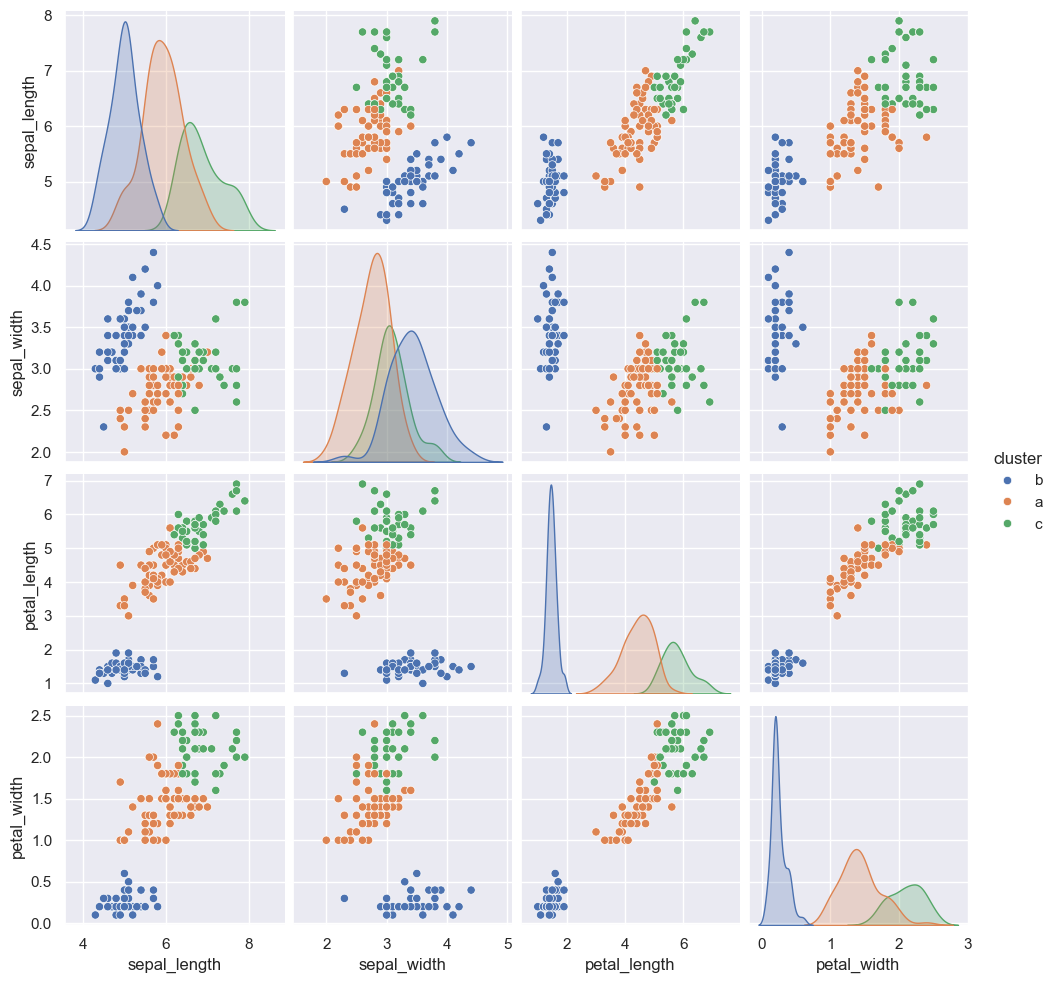
Observons nos clusters:
[15]:
sns.pairplot(X, hue="cluster")
[15]:
<seaborn.axisgrid.PairGrid at 0x29544cb6da0>
[ ]:
2.3.2 Scipy
Pour faire la même chose avec scipy, il suffit de prendre notre Z :
[16]:
Z[:10]
[16]:
array([[1.01000000e+02, 1.42000000e+02, 0.00000000e+00, 2.00000000e+00],
[7.00000000e+00, 3.90000000e+01, 1.00000000e-01, 2.00000000e+00],
[0.00000000e+00, 1.70000000e+01, 1.00000000e-01, 2.00000000e+00],
[9.00000000e+00, 3.40000000e+01, 1.00000000e-01, 2.00000000e+00],
[1.28000000e+02, 1.32000000e+02, 1.00000000e-01, 2.00000000e+00],
[1.00000000e+01, 4.80000000e+01, 1.00000000e-01, 2.00000000e+00],
[4.00000000e+00, 3.70000000e+01, 1.41421356e-01, 2.00000000e+00],
[1.90000000e+01, 2.10000000e+01, 1.41421356e-01, 2.00000000e+00],
[2.90000000e+01, 3.00000000e+01, 1.41421356e-01, 2.00000000e+00],
[5.70000000e+01, 9.30000000e+01, 1.41421356e-01, 2.00000000e+00]])
Ensuite on défini le nombre de clusters que l’on souhaite:
[17]:
k=3
On applique ensuite la fonction fclustersde scipypour définir les clusters :
[18]:
clusters = fcluster(Z, k, criterion='maxclust')
clusters
[18]:
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 2, 2, 2, 2, 3, 2, 2, 2,
2, 2, 2, 3, 3, 2, 2, 2, 2, 3, 2, 3, 2, 3, 2, 2, 3, 3, 2, 2, 2, 2,
2, 3, 3, 2, 2, 2, 3, 2, 2, 2, 3, 2, 2, 2, 3, 2, 2, 3], dtype=int32)
Ensuite on peut faire les représentations graphiques comme avec scikit-learn!
[ ]: